水分・厚さ計の測定原理について
1. 分光特性グラフと吸収強度(ランベルト・ベールの法則)
特定波長の赤外線は分子(原子)に吸収される特性を持っています。この波長はその分子を構成する原子やその結合状態により吸収される波長が異なってきます。
下に示すグラフは、赤外線の吸収(透過率)を縦軸に、波長(µm)を横軸にして表した分光特性グラフの一例です。
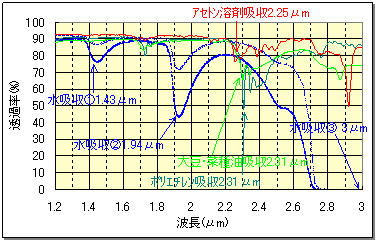
水の吸収特性や、溶剤、フィルム、油など、それぞれ違った特性を表しています。
またこの吸収特性は、その物質の量(厚み)に応じて吸収が強くなります。
これはランベルト(ランバー)・ベールの法則として次式で表されます。
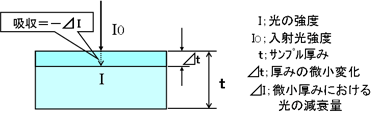
減衰量⊿I=-α・I・⊿t (α;吸収係数、物質、波長で決まる定数)
→ dI=-α・I・dt 両辺をtで積分(t=0~t)
赤外線の強度 I=I0・e^(-α・t)
チノーの赤外線水分・厚さ計は、この赤外線が物質(官能基)に固有の波長を吸収する特性、およびその量(厚み)により吸収量が変わることを利用し、物質中の各成分量を計測しています。
下に示すグラフは、赤外線の吸収(透過率)を縦軸に、波長(µm)を横軸にして表した分光特性グラフの一例です。

水の吸収特性や、溶剤、フィルム、油など、それぞれ違った特性を表しています。
またこの吸収特性は、その物質の量(厚み)に応じて吸収が強くなります。
これはランベルト(ランバー)・ベールの法則として次式で表されます。

減衰量⊿I=-α・I・⊿t (α;吸収係数、物質、波長で決まる定数)
→ dI=-α・I・dt 両辺をtで積分(t=0~t)
赤外線の強度 I=I0・e^(-α・t)
チノーの赤外線水分・厚さ計は、この赤外線が物質(官能基)に固有の波長を吸収する特性、およびその量(厚み)により吸収量が変わることを利用し、物質中の各成分量を計測しています。
2. センサ内部構造
水分・厚さ計の内部構成を以下に示します。
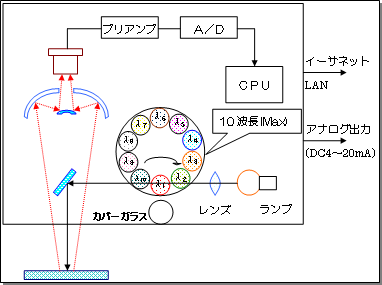
光源ランプから照射された光は、光学フィルターを通り特定波長だけ選別され物質に照射されます。照射された赤外線は計測対象(官能基)の振動により吸収され、減衰した反射光を凹面鏡にて再度集光し受光素子に入射されます。
またこの光学フィルターはモーターにて回転し、波長の異なる赤外線を断続的(パルス波)にて照射し、受光した赤外線は検出素子にて電気信号に変換され、各波長データをデジタル化し、吸光度信号を出力します。

光源ランプから照射された光は、光学フィルターを通り特定波長だけ選別され物質に照射されます。照射された赤外線は計測対象(官能基)の振動により吸収され、減衰した反射光を凹面鏡にて再度集光し受光素子に入射されます。
またこの光学フィルターはモーターにて回転し、波長の異なる赤外線を断続的(パルス波)にて照射し、受光した赤外線は検出素子にて電気信号に変換され、各波長データをデジタル化し、吸光度信号を出力します。
3. 吸光度演算について
当社の水分・厚さ計の吸光度出力は主に以下の出力となります。
①2波長比率演算
吸収波長λs、比較波長λr(吸収の少ない基準波長)の2波長にて
吸光度X= K1-λs/λr
K1;規格化定数(≒1)
吸光度X= K1-λs/λr
K1;規格化定数(≒1)
②3波長比率演算
吸収波長λs、比較波長をλr1、λr2の2波長使用
吸光度X= K1-λs/(α・λr1+(1-α)・λr2)
K1;規格化定数(≒1)、α;波長重み定数(0<α<1)
吸光度X= K1-λs/(α・λr1+(1-α)・λr2)
K1;規格化定数(≒1)、α;波長重み定数(0<α<1)
③重回帰演算
搭載している赤外線の各波長をλ1~λnとし、吸収特性が指数関数となることから各波長データの対数をとり以下の式で演算
成分値Y=a0+a1・Log(λ1)+a2・Log(λ2)+・・・an・Log(λn)
(水分、厚み、溶剤・・etc)
成分値Y=a0+a1・Log(λ1)+a2・Log(λ2)+・・・an・Log(λn)
(水分、厚み、溶剤・・etc)
①の2波長比率演算は、吸収量を基準となる波長との比率を取ることで、外乱要素となる、外来光・測定距離・光路上の粉塵・表面状態の変動、等の光量の絶対値の変動となる外乱をなるべく軽減できる利点があります。
また②の3波長比率演算は、2波長の発展型でさらにサンプルの表面状態や色、含有成分比率等の違い(当社では地合の違いと称している)に強い利点があります。
この比率演算による吸光度演算方法では、さらにこの吸光度を用いて検量線を作成し、求める成分値を算出します。
③の重回帰演算では、この式の係数を決定すれば直接求める成分値を出力できます。この重回帰演算は求める成分が、単一の変動量(1つの吸収波長)だけで表されず、複数(水分や厚さの吸収波長)の影響を受ける(干渉しあう)場合に、各要素(波長データ)を取り入れて求める方法で、一般に多変量を扱う場合の統計数学処理などに使われる演算方式です。この重回帰演算の係数を求めるには、実測数値を当てはめ、連立正規方程式の形にして求めていきます。
また複数の成分を同時に計測する場合、この重回帰演算の係数を成分ごとに当てはめることで、同時水分・厚さ測定が可能となります。
また②の3波長比率演算は、2波長の発展型でさらにサンプルの表面状態や色、含有成分比率等の違い(当社では地合の違いと称している)に強い利点があります。
この比率演算による吸光度演算方法では、さらにこの吸光度を用いて検量線を作成し、求める成分値を算出します。
③の重回帰演算では、この式の係数を決定すれば直接求める成分値を出力できます。この重回帰演算は求める成分が、単一の変動量(1つの吸収波長)だけで表されず、複数(水分や厚さの吸収波長)の影響を受ける(干渉しあう)場合に、各要素(波長データ)を取り入れて求める方法で、一般に多変量を扱う場合の統計数学処理などに使われる演算方式です。この重回帰演算の係数を求めるには、実測数値を当てはめ、連立正規方程式の形にして求めていきます。
また複数の成分を同時に計測する場合、この重回帰演算の係数を成分ごとに当てはめることで、同時水分・厚さ測定が可能となります。
4. 検量線について
3項①、②で求めた2(水分%、厚みμm、溶剤%・・etc)の変化に応じ増減する変数であり、成分量そのものではありません。
この吸光度値を求める成分量にするために検量線が必要になってきます。
検量線とは、予め測定対象のサンプルを測定する範囲にて何水準か振って水分・厚さセンサにて計測し、その吸光度値(X値)と、実測データから最小自乗法(誤差がもっも小さくなる回帰式を求める手法)にて求めた式のことです。
<検量線データ>
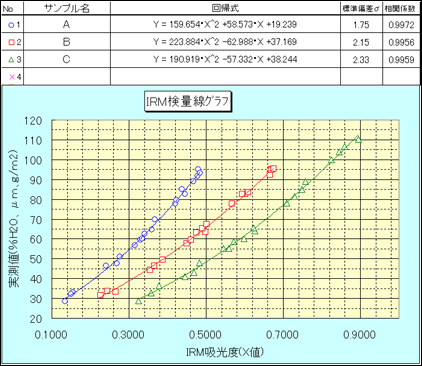
検量線は基本的に品種ごとに作成します。作成した検量線は本センサにMax99本まで格納でき、品種が変わるごとに検量線のチャンネルを切り替えて使用します。
*回帰演算式、標準偏差、相関係数の求め方へのリンク
この吸光度値を求める成分量にするために検量線が必要になってきます。
検量線とは、予め測定対象のサンプルを測定する範囲にて何水準か振って水分・厚さセンサにて計測し、その吸光度値(X値)と、実測データから最小自乗法(誤差がもっも小さくなる回帰式を求める手法)にて求めた式のことです。
<検量線データ>

検量線は基本的に品種ごとに作成します。作成した検量線は本センサにMax99本まで格納でき、品種が変わるごとに検量線のチャンネルを切り替えて使用します。
*回帰演算式、標準偏差、相関係数の求め方へのリンク
参考資料1. 検量線データと、ランベルト(ランバー)・ベールの法則に基づく吸光度値との関係について
前項の検量線データでは、実測値Yと、2(3)波長比率演算にて求めた吸光度X値との関係式を1~3次の多項式式にて求めています。これに対しランベルト(ランバー)・ベールの法則ではLog対数演算(厚さtで解いた時、t=-(1/α)・Log(I)+β)にて吸光度を求める式となっています。
以下に厚さ測定時を例としてランベルト(ランバー)・ベールの法則に基づく理論式から求めた吸光度と、当社で使用している「2波長比率演算」を使い2次、または3次回帰演算した場合の関係を下記グラフで示します。
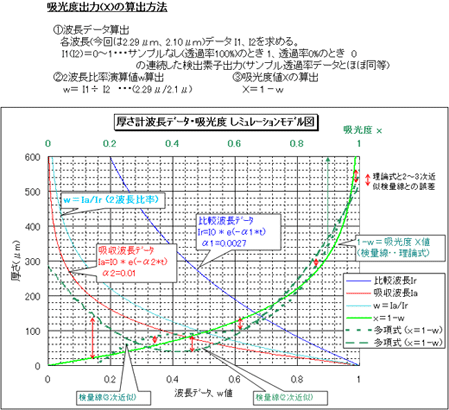
このモデル例における図中の赤矢印が理論式との誤差を表しています。
しかし、実際には、計測範囲が品種(ロット)ごとにある程度決まっており、その範囲で細かく回帰演算を行うことで、使用上問題にならない程度まで誤差を小さくすることが可能です。
また、重回帰演算については、各波長データの対数をとり(Logλn)演算しており、理論式と同じ演算方法を行っていますので、より回帰演算精度は向上します。
以下に厚さ測定時を例としてランベルト(ランバー)・ベールの法則に基づく理論式から求めた吸光度と、当社で使用している「2波長比率演算」を使い2次、または3次回帰演算した場合の関係を下記グラフで示します。

このモデル例における図中の赤矢印が理論式との誤差を表しています。
しかし、実際には、計測範囲が品種(ロット)ごとにある程度決まっており、その範囲で細かく回帰演算を行うことで、使用上問題にならない程度まで誤差を小さくすることが可能です。
また、重回帰演算については、各波長データの対数をとり(Logλn)演算しており、理論式と同じ演算方法を行っていますので、より回帰演算精度は向上します。
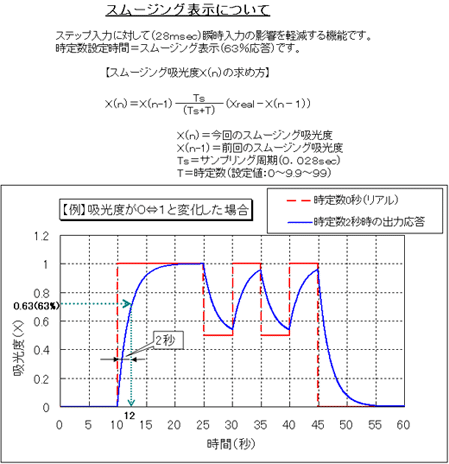
参考資料2. スムージング演算について
当社の水分・厚さ計はオンライン計測に主に使用されますが、オンラインにおいては数々の外乱外来光・測定距離・光路上の粉塵・表面状態の変動、等により測定データがフラツク要因となります。そのため当社では、下記のような演算処理を行い、これらの外乱を取り除き安定した計測を可能にしています。